- A.
- First measure the
f of a weak converging lens (
25
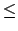 f
f 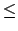 50 cm) and
of a strong converging lens (f
50 cm) and
of a strong converging lens (f 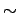 5 cm). The first lens (f large) typically
has the virtue of intercepting and focusing a fairly large area of light while the
second lens can be positioned to give a large virtual image (and hence magnification.)
Notice that if the first image, q1is at a point p2 > f2 with respect to the
second lens you get a real, erect second image.
If you are using the web-based
lab manual and desire a demonstration, click on the Inverting Telescope Demo button
immediately below.
5 cm). The first lens (f large) typically
has the virtue of intercepting and focusing a fairly large area of light while the
second lens can be positioned to give a large virtual image (and hence magnification.)
Notice that if the first image, q1is at a point p2 > f2 with respect to the
second lens you get a real, erect second image.
If you are using the web-based
lab manual and desire a demonstration, click on the Inverting Telescope Demo button
immediately below.
Use you will use these two lenses to construct an astronomical (inverting) telescope. As an object, use the white board and scale while illuminated by a bright light. As a procedure for measuring the magnification, vary the space between the objective L1 and the eyepiece L2 until the virtual image I2 of scale S seen through L2 lies in the plane of S (i.e. p1 + d = | q2|). As a sensitive test of this there should be no parallax between the scale as seen directly by your eye 2 and the scale image seen by eye 1 thru the telescope as shown in Fig. 2. Generally a person will adjust the eyepiece so that the virtual image appears at the distance of most distinct vision (
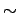 25 cm).
25 cm).
- B.
Adjust the telescope direction until these images superimpose (as in Fig. 3). The number of divisions on the scale as viewed directly (by eye 2) which fall in one division of the image as seen through the telescope (by eye 1) is clearly the magnifying power of the telescope.
Compare your measured magnification M with that calculated for an astronomical telescope, namely M = f1/f2 where f1 is the focal length of the objective and f2 that of the eye piece. Why are the two different? Calculate the magnification from the actual measured object and image distances. Compare with the measured M.
Figure 3:![\includegraphics[height=1.8in]{figs/l3-03.eps}](img262.gif)
- A.
- Measure the focal length, f, of a second strong converging lens and use it as
the inverting lens L3 (Fig. 4) to form an erecting telescope. L2 must be adjusted
to give a real image, I2.
Notice that
varying the space between
I1 and the inverting lens L3 changes the magnification.
If you are using the web-based
lab manual and desire a demonstration, click on the Erecting Telescope Demo button
immediately below. In this simulation your are now able to readjust both the positions and
focal lengths!
- B.
- What position of the inverting lens makes the shortest possible telescope, (i.e. it makes the distance between I1 and I2 a minimum)?
|
Compound microscope: Use the two strong converging lenses to form a compound microscope. |
Figure 5: Setup for compound microscope.
![\includegraphics[height=2.in]{figs/l3-05.eps}](img264.gif)
|
![\includegraphics[height=2.2in]{figs/l3-01.eps}](img260.gif)
![\includegraphics[height=1.6in]{figs/l3-02.eps}](img261.gif)
![\includegraphics[height=2.0in]{figs/l3-04.eps}](img263.gif)
![\includegraphics[height=1.8in]{figs/l3-06.eps}](img265.gif)
![\includegraphics[height=2.2in]{figs/l3-07.eps}](img266.gif)
![\includegraphics[height=1.3in]{figs/l3-08.eps}](img267.gif)